05. Logische Verknüpfungen

Logische Verküpfungen

In der Digitaltechnik werden logische Steuersignale zusammengeführt und nach festgelegten Gesetzen der Booleschen Algebra ausgewertet. Diese Algebra kommt mit zwei Konstanten 0 und 1 und den Operatoren UND, ODER sowie NICHT aus. Jede Variable kann nur den Wert 0 oder 1 annehmen. Das Ergebnis ist ebenfalls als Variable zu betrachten und besitzt daher auch nur die Werte 0 oder 1. Für die Schreibweise der Operatorensymbole gibt es keine einheitliche Regelung.

Die logischen Grundverknüpfungen

Operator	Symbol			Beispiel
	Programm	Logisch	Mengenlehre
UND/AND/Konkunktion	$\&\&$	$\wedge$	$\cap$	Schutzschalter: Beide Taster an Kettensäge betätigt werden, damit sie sägt.
ODER/OR/Disjunktion	$\mid\mid$	$\vee$	$\cup$	Türklingel: Vor dem Haus oder vor der Wohnungstür klingeln, damit es läutet
NICHT/NOT/Negation	$!x$	$\neg$x	$\bar{x}$	Autofahren, wenn nicht betrunken

Mengendarstellung der Grundverknüpfungen

AND	OR	NOT
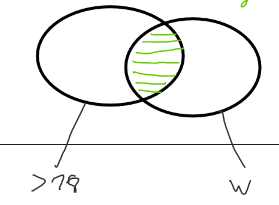
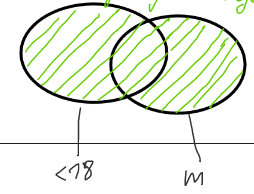
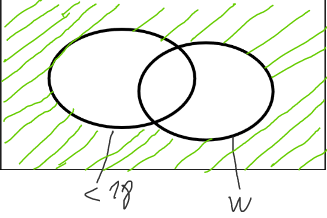
Alle Schüler, die > 18 Jahre und weiblich sind	Alle Schüler, die < 18 Jahre oder männlich sind	Alle Schüler, die nicht weiblich sind
Schnittmenge	Vereinigungsmenge	Subtraktion

Darstellung der Grundverknüpfungen

UND bzw AND

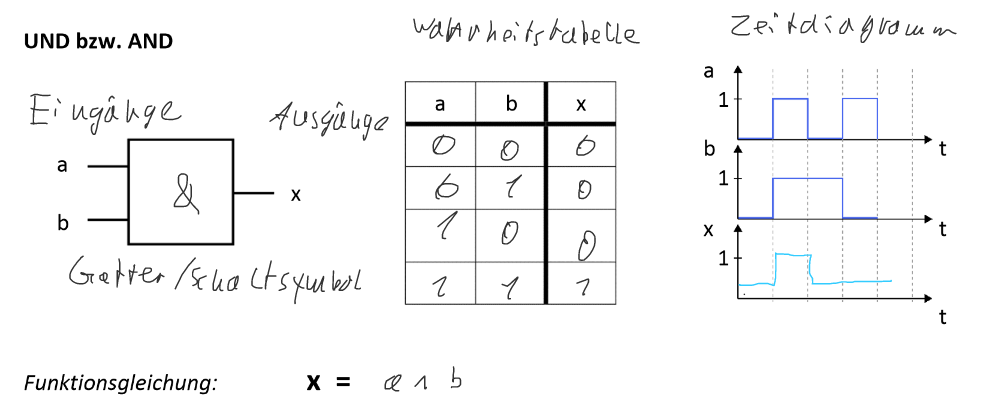
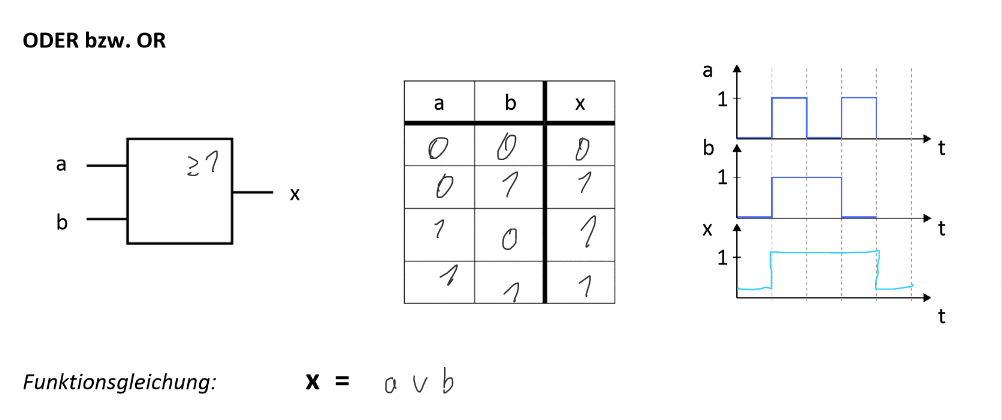
ODER bzw OR

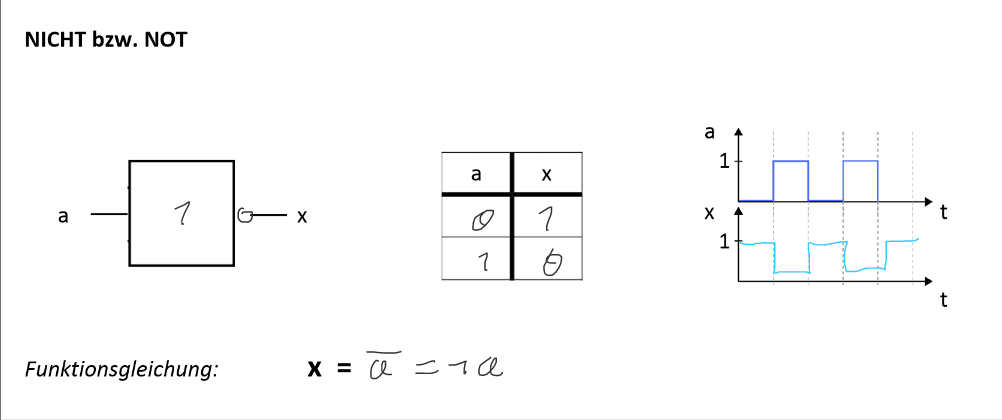
NICHT bzw NOT

Weitere Verknüpfungen

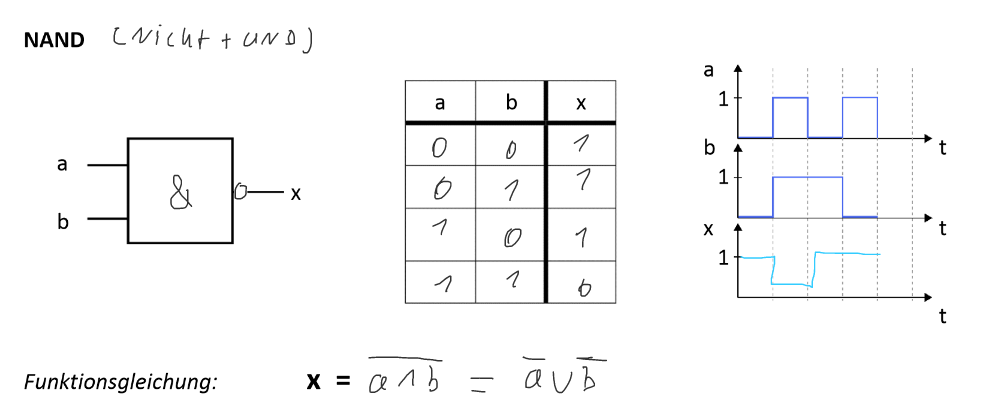
Nicht Und bzw NAND

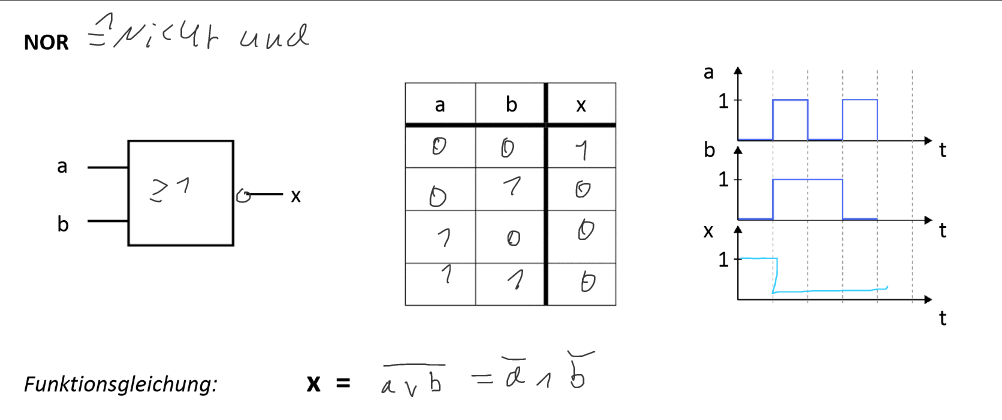
Nicht Oder bzw NOR

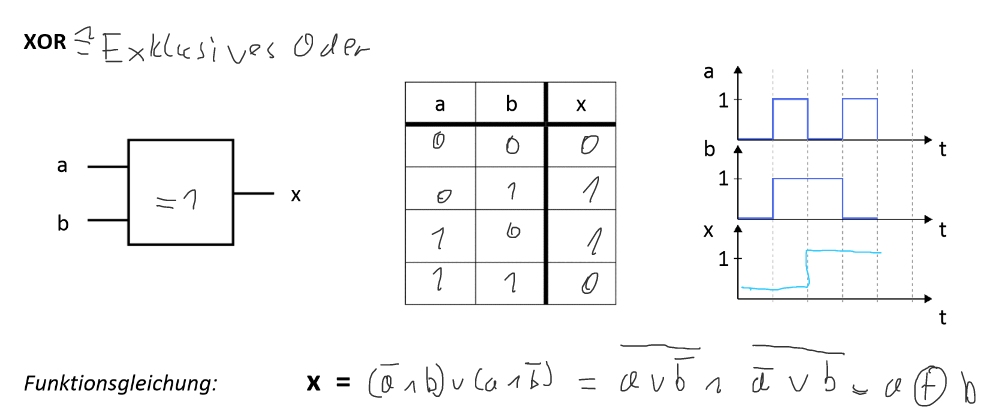
Exklusiv Oder bzw XOR

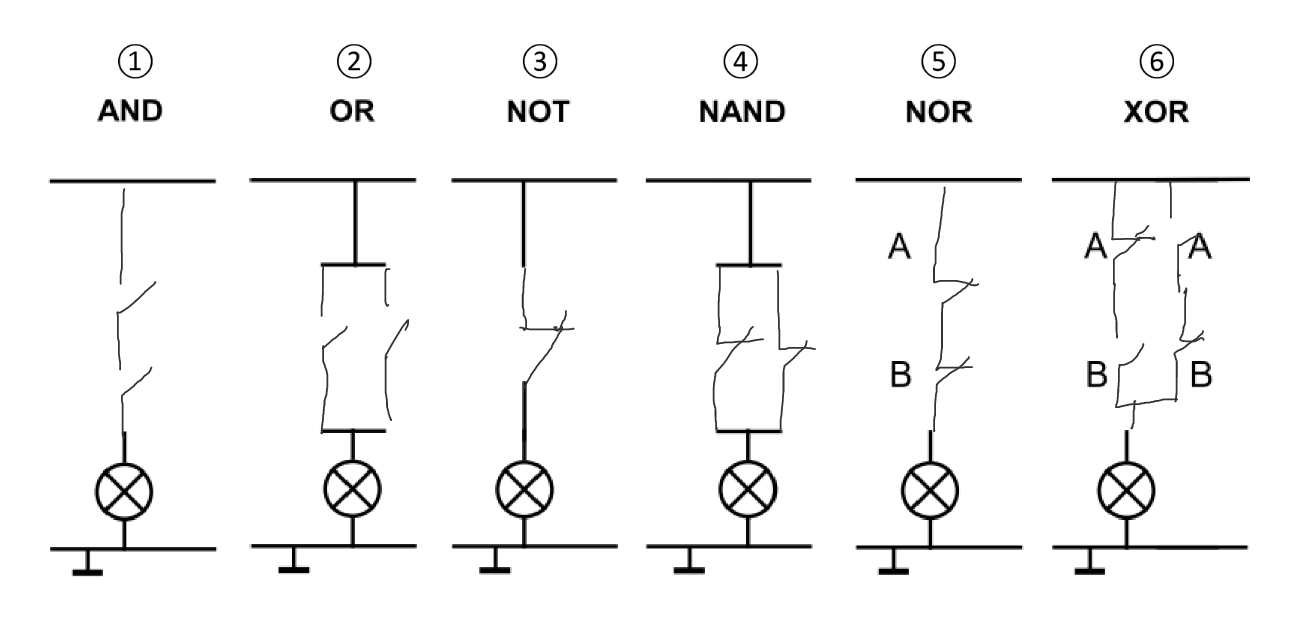
Kontaktschaltung

Eine Kontaktschaltung ist eine Schaltung bei der der Verbraucher nur aktiv werden kann, wenn Strom fließt. Die Schaltung erfüllt im Regelfall einen Zweck wie bspw. das mehrere Schalter gedrückt sein müssen. Mit einer Kontaktschaltung kann man ebenfalls eine boolesche Gleichung visualisieren oder umgekehrt die boolesche Gleichung beschreibt die Schaltung. Im folgenden sind die Kontaktschaltungen zu sehen, welche die Grundglieder bilden.

Lehrsätze und Umformungen

AND	OR	NOT
$a \wedge 0 = 0$	$a \vee 0 = a$	$\neg\neg a = a$
$a \wedge 1 = a$	$a \vee 1 = 1$
$a \wedge a = a$	$a \vee a = a$
$a \wedge \neg a = 0$	$a \vee \neg a = 1$

Gesetze der Schaltalgebra

Name	Formel	Kommentar
Bindung der Operatoren	$a \vee b \wedge c = a \vee (b \wedge c)$	UND vor ODER
Kommutativgesetz	$a \vee b = b \vee a$	Vertauschung bei
	$a \wedge b = b \wedge a$	gleichen Operatoren möglich
Assoziativgesetz	$(a \vee b) \vee c = a \vee (b \vee c)$	Bei gleichen Operatoren ist
	$(a \wedge b) \wedge c = a \wedge (b \wedge c)$	die Reihenfolge egal.
Distributivgesetz	$a \wedge (b \vee c) = (a \wedge b) \vee (a \wedge c)$	“Ausklammern”
	$a \vee (b \wedge c) = (a \vee b) \wedge (a \vee c)$
Gesetz von De Morgan	$\overline{a \overline b} = \overline{a} \vee \overline{b}$
	$\overline{a \vee b} = \overline{a} \wedge \overline{b}$
	$a \wedge b = \overline{\overline{a \wedge b}} = \overline{\overline{a} \vee \overline{b}}$
	$a \vee b = \overline{\overline{a \vee b}} = \overline{\overline{a} \wedge \overline{b}}$